앞 글에서 호언장담 했듯이 “함수형 프로그래밍”에 대해서 기본부터 살펴보자.

우선 함수란 무엇인가? 우리는 함수가 뭔지 이미 알고있다. 중학교 때 배웠던 기억을 더듬에 보자. 함수의 정의는 무엇인가?

…

기억이 나지 않을 가능성이 높다. 기억이 났더라도 엄밀한 의미의 정의와 분명 차이가 있을 거다. 사실 나도 기억나지 않는다. 수학 전공이 아닌 이상 우리는 함수의 명확한 정의를 알지 못한다. 하지만 시험에서 정답을 고르는데는 정말 익숙해질 수 있는 대한민국 교육 덕분에 어떤 함수가 잘못된 함수인지는 기억할 수 있다.

어떤 함수가 정의역을 가지고 치역을 가진다고 상상해보자. 정의역과 공역(및 치역)은 말풍선 같은 위아래로 길쭉한 타원형으로 표현되고, 그 안에 요소(꼭 숫자일 필요는 없지만 중학교 교육 상 숫자로 상상하자) 들어있다. 그리고 정의역의 각 요소는 하나씩 화살표와 연결되어 있다. 이 화살표들은 왼쪽의 공역 타원형 내의 요소들과 연결된다. 공역 요소들 중에서 화살표에 맞은 애들을 묶어서 치역이라고 불렀다. 이 그림의 위쪽 가운데 필기체로 f 또는 g라고 적혀있었을 것이다.

우리는 이걸 함수라고 배웠다.

그렇다면 잘못된 함수는? 크게 두가지가 보통 오답으로 선택지에 있었던 걸로 기억한다. 하나는 정의역 요소 중 하나에서 화살표가 나가지 않는 것 이다. 다른 하나는 정의역 요소 하나가 화살표 두개와 연결되어 있는 것 이다.

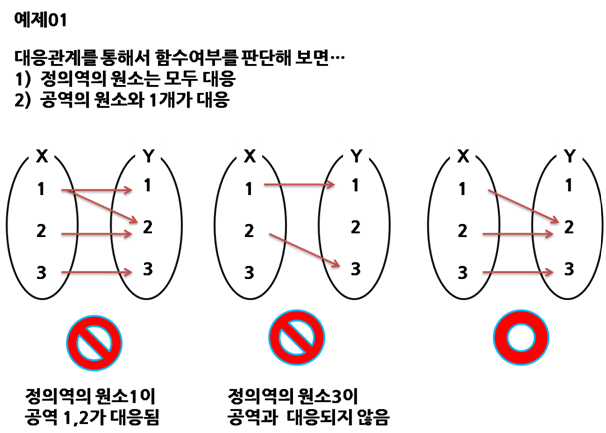
실제로 교육 블로그에서 퍼온 사진이다.
출처: http://j1w2k3.tistory.com/

이 두 경우는 함수가 아니다. 라고 우리는 배웠고 문제를 풀어왔다.

중학교 수학에서 다시 컴퓨터 세계로 돌아와보자. 프로그래밍 언어(C, JAVA, PYTHON을 떠올려보시라. 완벽한 함수형 언어도 있으니까. 이하 언급하는 프로그래밍 언어는 함수형 언어를 제외한 것으로 생각해주자)의 함수는 함수인가? 이 프로그래밍 언어가 지원하는 function 혹은 module은, 수학적 의미의 함수와 같은가?

정답은 ‘같지 않다’이다. 수학적 함수와 프로그래밍 언어의 함수는 같지않다. 유명한 예를 들어서 어떻게 다른지 보자.

A: 숫자 1과 2가 있고, 1에다 2를 더하면?
B: 3이지.
A: 그럼 아까 1에다 4를 더하면?
B: 5지.
A: 아냐 7이야. 왜냐하면 아까 1에다 2를 더해서 3이 되었기 때문이지.

이런 말도 안되는 주장이 있나? 그러나 프로그래밍 세계에서 이는 빈번히 일어난다. 위의 대화는 다음과 같은 C코드로 써볼 수 있다.

int a = 1;
int b = 2;
a = a + b; // 3

printf("%d", a + 4); // this prints 7, because the A 'became' 3.

프로그래머는 5를 출력하길 원했으나, 실제로 나오는 값은 7이다.

이 예시를 보고 당신은 이런 바보같은 프로그래머가 어딨냐고 코웃음 칠지도 모른다. 억지스러운 예라고 말이다. 하지만 위의 코드는 가장 간략화된 형태의 버그일 뿐이다. 요즘의 프로그램은 수십줄 단위에 그치지 않는다. 한사람이 관리하는 코드만 몇만줄을 쉽게 넘어가고, 여러사람이 협업하는 경우 그 규모는 이미 인간의 뇌의 관리범위를 넘어간다. 이런 상황에서 어떤 특정 모듈이 문제를 일으키는지 찾기란 정말 쉽지 않다. 특히 그게 오래된 코드일수록, 다른 사람이 쓴 코드일수록 더 그렇다. 위의 예시의 경우, int a = 1;, int b = 2;, printf("%d", a + 4);는 문제가 없다. 중간의 삽입된 코드가 문제를 일으킨 것이다. 이 때 기존의 코드는 ‘삽입된 코드’에 보이지 않는 의존성을 갖는다. 그리고 이 보이지 않는 의존성은, 모든 경우(100%라고 확신한다)의 프로그래밍에서 반드시 문제의 원인이 된다.

위의 코드의 경우도, 만일 a = a + b;가 존재하지 않는다면 별 문제없이 작동한다. 하지만 모종의 이유로 중간에 a = a + b;가 들어가고 말았기에 오류가 난 것이다. 프로그램 유지보수를 하다 보면, 중간에 최초에는 존재하지 않던 코드가 어떤 이유에서 들어가는 것은 매우 일반적인 현상 이다. 그리고 그 삽입된 코드가 원래의 동작에 ‘어떤’ 영향을 미칠지는, 복잡한 프로그램에서 예상하기란 거의 불가능 에 가깝다. 아니, 사실 이론적으로 불가능하다. 따라서 프로그래밍 필드는 수많은 테스팅 기법들을 발달시켜 왔으며, TDD, BDD니 하는 온갖 기법들로 첨가, 변형, 제거되는 코드들로 인한 오류를 제거하기위해 애쓴다. 하지만 이는 코드 결과를 통제하고자 하는 시도이지, 근본적인 문제를 해결하지 못한다. 근본적인 문제는 코드간의 보이지 않는 의존성 이며, 이를 해결해야만 버그를 최소화 할 수 있다! (이 경우 보이지 않는 의존성은 ‘메모리 공간’에 의해 발생하고 있다)

결국, 프로그래밍의 함수는 일단은 위에서 살펴본 점에서 실제 함수와 다르다. 이런 다른 점들이(하나가 아니다) 수학의 엄밀성을 컴퓨터에서는 불가능하게하고, 프로그래머가 예상하지 못한 버그를 발생시킨다. 함수형 프로그래밍은 “수학적 함수”와 “프로그래밍적 함수”의 차이를 최대한 제거하여 컴퓨터 프로그래밍이 수학에 가까운 엄밀성을 가질 수 있도록, 그래서 버그를 최소화 할 수 있도록 하기 위한 도구 이다. 함수형 프로그래밍은 프로그래머를 괴롭히기 위한(쏟아지는 자바스크립트 새로운 프레임워크들 처럼. javascript fatigue like.) 것이 아니다! 함수형 프로그래밍은 여러분을 돕기 위해 태어났다.

함수평 프로그래밍은 인간이 ‘보다’ 익숙한(수학적 사고가 인간의 본성은 아니니까), 초등학교때부터 훈련되어온 수학적 사고방식으로 프로그래밍을 할 수 있게 해준다. 기존에 C, JAVA등은 인간이 컴퓨터적으로 사고하도록 개조되기를 요구해 왔다. 사상 개조가 있어야만 가능했던 프로그래밍을, 이미 익숙한 수학적 사고만으로 가능하게 한다. 그런 의미에서 함수형 프로그래밍은 쉽고 직관적이다.

위의 예시에서 말하는 것 같은 이유로 수학적 함수와 프로그래밍의 함수가 다른 점이 있다는 것은 알겠다면, 좀 더 포괄적으로 컴퓨터와 수학이 어떻게 다른지 살펴볼 필요가 있다. 수학과 컴퓨터는 어떻게 다른가? 어떤 다른 점이 프로그래머를 편하게/곤란하게 하는가?

수학과 프로그래밍의 차이가 명백해지면, 우리는 그 지점으로부터 함수형 프로그래밍이 지향하는바를 이해할 수 있게 된다. 그러고 나면, 왜 ‘순수함수’가 필요한지, 왜 ‘불변형’이 필요한지, 왜 고차함수, 1급함수, 커링 등이 필요한지 찬찬히 이해하게 된다.

우선 다음 장에서는 수학과 프로그래밍의 차이를 알아보고, 그 다음장 부터 함수형 프로그래밍의 특징을 본격적으로 다루어 보겠다. 다시 한 번 말하지만, 함수형 프로그래밍을 여러분은 이미 알고 있다. 어떻게? 함수는 수학이니까!